Poids et masse: équilibre d'un objet:III-Equilibre d'un objet soumis à deux forces.
- Un objet soumis à deux forces F1 et F2 est en équilibre si :
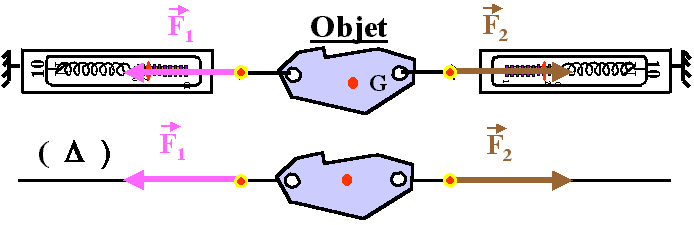
- Les deux forces ont la même direction, la même intensité mais de sens opposés.
- Les deux forces ont la même intensité et le même sens mais des directions opposées.
- Les deux forces ont la même direction, le même sens mais des intensités différentes.
- Que va-t-il se passer si l'intensité de la force F1 est supérieure à l'intensité de la force F2 ?Les forces gardent le même sens et la même direction.
- L'objet va se déplacer horizontalement et à gauche.
- L'objet va se déplacer horizontalement et à droite.
- L'objet ne va pas se déplacer .
- Que va-t-il se passer si l'intensité de la force F1 est inférieure à l'intensité de la force F2 ?Les forces gardent le même sens et la même direction.
- L'objet va se déplacer horizontalement et à gauche.
- L'objet va se déplacer horizontalement et à droite.
- L'objet ne va pas se déplacer .
- Que va-t-il se passer si on supprime les deux forces F1 et F2 .
- L'objet va chuter verticalement.
- L'objet va chuter sans une direction précise.
- L'objet restera au même endroit .
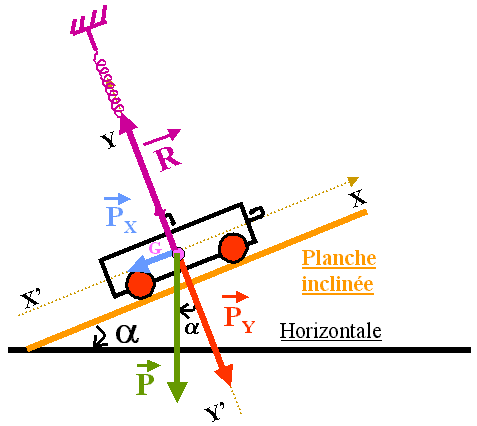
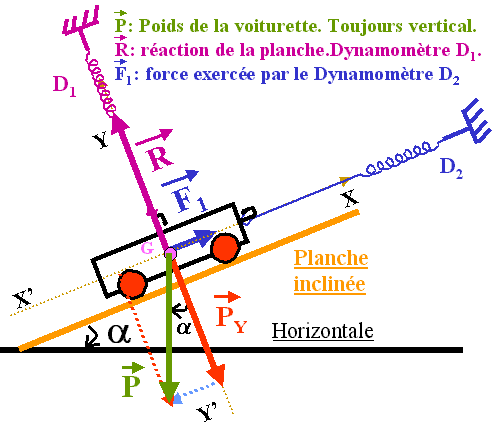
- La voiturette est en équilibre car:
- Sur l'axe XX': F1 et Py même direction, même intensité et de sens opposés.
Sur l'axe YY': R et Px même direction, même intensité et de sens opposés. - Sur l'axe XX': F1 et Px même direction, même intensité et de sens opposés.
Sur l'axe YY': R et Py même direction, même intensité et de sens opposés. - Sur l'axe XX': R et Px même direction, même intensité et de sens opposés.
Sur l'axe YY': F1 et Py même direction, même intensité et de sens opposés.
- La voiturette est en équilibre car elle est tirée par F1 et le poids P se décompose en:
- Py sur l'axe XX'et Px sur l'axe YY'. Car on a réalisé une projection orthogonale de P sur les axes.
- Py sur l'axe XX'et Px sur l'axe YY'.Car on a réalisé une projection orthogonale de P sur les axes.
- Px sur l'axe XX'et Py sur l'axe YY'.Car on a réalisé une projection orthogonale de P sur les axes.
- On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?
- Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette est tirée vers la gauche. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette la voiturette est tirée vers la droite. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette reste immobile.
- On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?
- Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va glisser. - Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va casser la planche. - Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va descendre.
- On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?
- Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette est tirée vers la droite. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette est tirée vers la gauche. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette reste immobile.
- Allons chercher du " côté" de Monsieur Pythagore.
On montre que l'angle A G B = a ( Triangle rectangle dont deux côtés sont perpendiculaires)
On donne les relations trigonomètriques dans le triangle AGB.
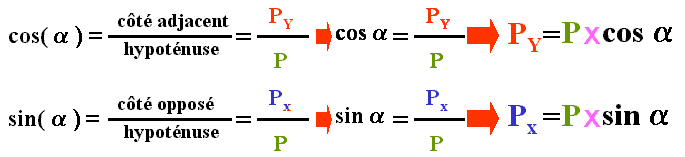
La voiturette est en équilibre, elle a une masse m = 10kg , on donne g = 10N/kg . a = 30°.
Calculer P, Px, Py et déduire F1 , R
Calculette- P= m x g = 100N, Py = R = P x sin a=50N , Px = F1 = P x cos a=86,6N.
- P= m x g = 100N, Px = R = P x sin a=86,6N , Py = F1 = P x cos a=50N.
- P= m x g = 100N, Px = R = P x sin a=50N , Py = F1 = P x cos a=86,6N.
- Un objet soumis à deux forces F1 et F2 est en équilibre si :
- Les deux forces ont la même direction, la même intensité mais de sens opposés.
- Les deux forces ont la même intensité et le même sens mais des directions opposées.
- Les deux forces ont la même direction, le même sens mais des intensités différentes.
Que va-t-il se passer si l'intensité de la force F1 est supérieure à l'intensité de la force F2 ?Les forces gardent le même sens et la même direction.- L'objet va se déplacer horizontalement et à gauche.
- L'objet va se déplacer horizontalement et à droite.
- L'objet ne va pas se déplacer .
Que va-t-il se passer si l'intensité de la force F1 est inférieure à l'intensité de la force F2 ?Les forces gardent le même sens et la même direction.- L'objet va se déplacer horizontalement et à gauche.
- L'objet va se déplacer horizontalement et à droite.
- L'objet ne va pas se déplacer .
Que va-t-il se passer si on supprime les deux forces F1 et F2 .- L'objet va chuter verticalement.
- L'objet va chuter sans une direction précise.
- L'objet restera au même endroit .
La voiturette est en équilibre car:- Sur l'axe XX': F1 et Py même direction, même intensité et de sens opposés.
Sur l'axe YY': R et Px même direction, même intensité et de sens opposés. - Sur l'axe XX': F1 et Px même direction, même intensité et de sens opposés.
Sur l'axe YY': R et Py même direction, même intensité et de sens opposés. - Sur l'axe XX': R et Px même direction, même intensité et de sens opposés.
Sur l'axe YY': F1 et Py même direction, même intensité et de sens opposés.
La voiturette est en équilibre car elle est tirée par F1 et le poids P se décompose en:- Py sur l'axe XX'et Px sur l'axe YY'. Car on a réalisé une projection orthogonale de P sur les axes.
- Py sur l'axe XX'et Px sur l'axe YY'.Car on a réalisé une projection orthogonale de P sur les axes.
- Px sur l'axe XX'et Py sur l'axe YY'.Car on a réalisé une projection orthogonale de P sur les axes.
On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?- Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette est tirée vers la gauche. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette la voiturette est tirée vers la droite. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': Py est seule , la voiturette reste immobile.
On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?- Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va glisser. - Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va casser la planche. - Sur l'axe XX': Px et F1 même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe YY': Py est seule , la voiturette va descendre.
On suppose que la voiturette est soumise aux seules forces schématisées, quel sera son état?- Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette est tirée vers la droite. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette est tirée vers la gauche. - Sur l'axe YY': R et Px même direction, même intensité et de sens opposés; elles se compensent.
Sur l'axe XX': F1 est seule , la voiturette reste immobile.
Allons chercher du " côté" de Monsieur Pythagore.On montre que l'angle A G B = a ( Triangle rectangle dont deux côtés sont perpendiculaires)On donne les relations trigonomètriques dans le triangle AGB.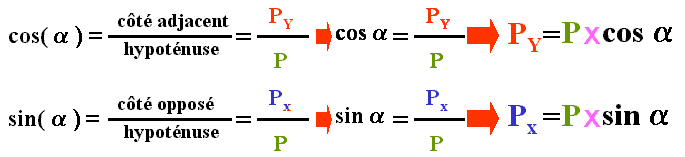La voiturette est en équilibre, elle a une masse m = 10kg , on donne g = 10N/kg . a = 30°.
Calculer P, Px, Py et déduire F1 , R
Calculette- P= m x g = 100N, Py = R = P x sin a=50N , Px = F1 = P x cos a=86,6N.
- P= m x g = 100N, Px = R = P x sin a=86,6N , Py = F1 = P x cos a=50N.
- P= m x g = 100N, Px = R = P x sin a=50N , Py = F1 = P x cos a=86,6N.